逻辑回归(Logistic Regression)是一种用于解决二分类(0 or 1)问题的机器学习方法
由于Sigmoid函数的函数性质:作用域是负无穷到正无穷,值域是(0,1),很适合二分类的场景,式子如下所示:
假设我们预测函数为y = θ * x1 + b
决策边界分为线性决策边界和非线性决策边界,如图所示:
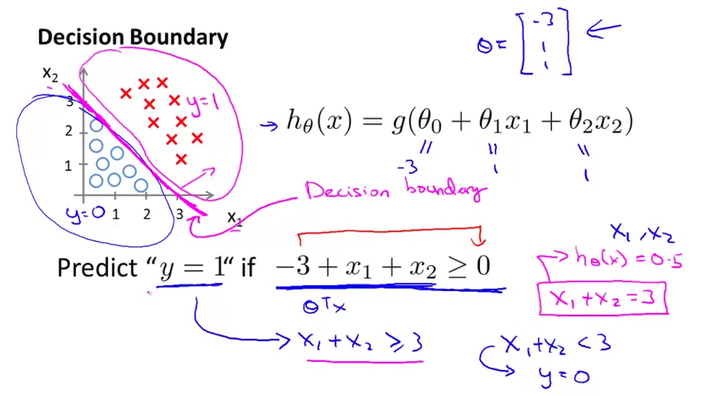

上面两张图很清晰的解释了什么是决策边界,决策边界其实就是一个方程,在逻辑回归中,决策边界由 θ^Tx=0 定义。
那么,问题: 如何确定Sigmoid函数的决策边界是线性还是非线性的?
另y = 1 - y,得到θ^Tx + b = 0, 线性
我们把Sigmoid函数用联合概率分布函数表达出来,可以写成以下公式:
P(y=1|x;θ)=hθ(x)
P(y=0|x;θ)=1−hθ(x)
似然函数为;
L(θ)=∏i=1mP(y(i)|x(i);θ)
对其通过log取对数简化,得到log似然函数:
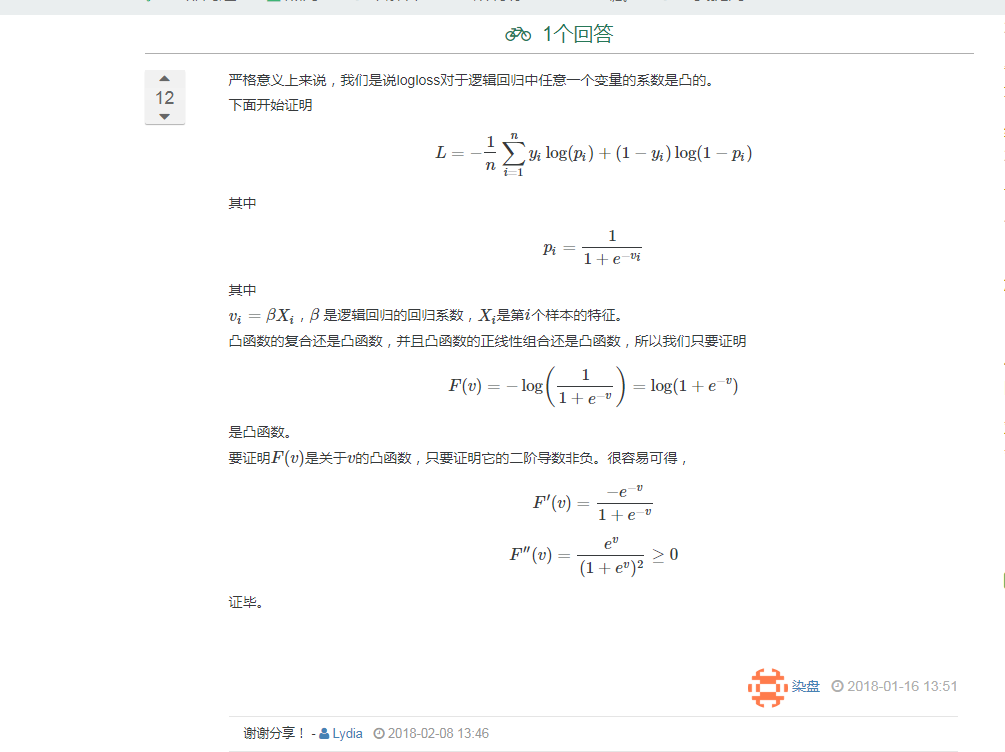
l(θ)=log(L(θ))=∑i=1my(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
L(θ)求最大值,转化为可以在l(θ)前加个负号,求式子后面的最小值
通过求导,梯度下降优化θ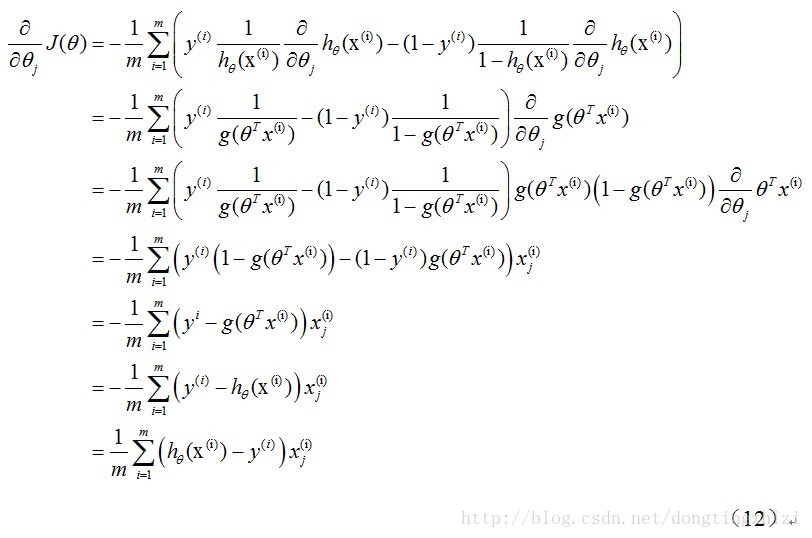
*如何证明log似然函数是凸函数?
有空手写求偏导一下