2019-04-23

从loss函数聊开根号的两种算法

初识loss函数

引用：函数（loss function）是用来估量模型的预测值f(x)与真实值Y的不一致程度，它是一个非负实值函数,通常使用L(Y, f(x))来表示，损失函数越小，模型的鲁棒性就越好。

举个例子：已知预测模型函数 f(x)和真实对应的产出值(Y)

损失函数可为 L(Y,f(X)) = (Y-f(X))^2

总结： loss函数依赖两个值，真实值Y，预测函数f(x),loss函数则是评判预测是否准确的函数

回归loss

例子中用的是回归loss中的一种，MSE，又叫L2函数，特点是可根据位置调整学习率，缺点是受噪点影响严重。
另一种常见的回归loss是MAE，利用绝对值评估，即L1函数，特点是噪点影响小，缺点是步调过于统一。
结合MAE和MSE而产生的Huber Loss，结合了两者的优点，规避了缺点，在y-f(x)小于一定值时使用MSE，大于一定值时使用MAE

L2损失是平滑函数，在求解其优化问题时有利于误差梯度的计算；L1损失对估计值和真实值之差取绝对值，对偏离真实值的输出不敏感，因此在观测中存在异常值时有利于保持模型稳定。-百度百科

分类loss

0-1
最简单的0-1分类缺点：不连续，非凸，优化困难
Logistic分类
Logistic是非常经典的一个回归模型，Logistic回归模型是0-1模型的代理loss,

0-1损失函数是一个不连续的分段函数，不利于求解其最小化问题，因此在应用可构造其代理损失（surrogate loss）。代理损失是与原损失函数具有相合性（consistency）的损失函数，最小化代理损失所得的模型参数也是最小化原损失函数的解。当一个函数是连续凸函数，并在任意取值下是0-1损失函数的上界时，该函数可作为0-1损失函数的代理函数

h θ (x) = g (θ T x) = 1 1 + e - θ T x

由此式可变形出log loss,又称log似然函数:

对该函数求导，令导函数等于0，该导函数没有解析解，但是可以用牛顿迭代求解。什么是牛顿迭代求解，回归主题，我们用开根号这个例子来列式解释。

牛顿迭代求解

牛顿迭代求解，是利用曲线的某个点的泰勒展开式来计算下一个更接近最接近最终解的中间点，反复迭代可以无限接近真实解。
例，利用牛顿迭代开根号：
先列出函数，我的理解是牛顿迭代最终效果是可对y=0场景求x值，
那么可列出 f(x) = x^2 - n ， f(x) = 0时，x值为n开根号的值
对该函数进行牛顿迭代：

该函数的导函数为 f’(x) = 2x
取任一点(x(n), y(n))
y(n) = x(n)^2 - n , 即点为(x(n), x(n)^2 - n), 该点的斜率为 2x(n)
该点的切线方程为： (y - (x(n)^2 - n))/(x - x(n)) = 2x(n)
化简为： y = 2(x(n))*x - x(n)^2 - n

令y = 0, 得到迭代方程 x = (x(n)^2 + n)/ 2*x(n)
取任一点x(n),用该迭代方程迭代，则能得到接近真实值的最终值

以上是用高中数学求迭代式，然后我们可以尝试高级一点，用泰勒展开式求迭代式：

$f (x) = f (x_{0}) + f^{'} (x_{0}) (x - x_{0}) + \frac{f^{″} (x_{0})}{2!} (x - x_{0})^{2} + \dots + \frac{f^{(n)} (x_{0})}{n!} (x - x_{0})^{n} + R_{n} (x)$

取一次项，即

可得迭代公式：

代入，得到 x(n+1) = x(n) - (x(n)^2 - n)/2x(n)
x(n+1) = (x(n)^2 + n)/2 x(n)

发现，辛辛苦苦求了半天的切线方程，用泰勒展开式分分钟搞定了有木有

梯度下降求解

梯度下降求解的思路是找最平缓的位置，根据这个思路列方程式: f(x) = (x^2-n)^2

根据梯度下降的式子，这边的思想精髓还没能吸收，(为什么一个值减去学习率*该点的导数，得到的值是什么意义？为什么能无限接近最终解)
先按照式子来。。

f’(x) = 4＊x^3 - 4＊n＊x = 4＊x(x^2 - n)

f(x1) = f(x0) - a * f’(x0)

假设n = 5 , x0 = 2, f(2) = 1 , a = 0.001, f’(2) = 8 (-1) = -8
t0 = 1 - 0.001 (-8) = 1.008
t1 = t0 - 0.001 * f’(t0)
….
无限迭代

写出py代码为：

def test(yn) :
     return 4.*np.power(yn,3)-4.*yn*5
y = 2
count = range(500)
for i in count:
    y = y - 0.001 * test(y)
    print(y)

运行500次后，可得接近值：

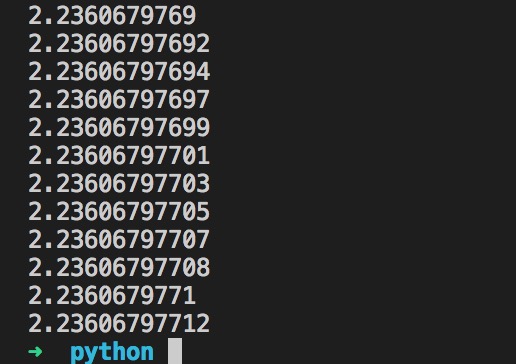
该思想精髓，留坑待补充
不过略微有一点思路，可以拿速度和加速度来强化理解，当速度趋近于匀速时，此时加速度为0，那么反向推倒，在由速度足够大到减速到匀速的这个过程中，任意取一点的速度，用足够短的时间(a 学习率)乘以此刻的加速度，得到另一个略微更趋近于匀速的速度，在新的速度上重新取加速度，重复以上过程，在逐渐接近匀速的过程中，每次重新取的点的加速度会越来越小，取无限次只会最终趋近匀速值，因为最后的加速度趋近于0，终将得到一个逼近值。